A) সংখ্যা পদ্ধতি (computer number system)
অতীতকালে মানুষ নিজের আঙ্গুল অথবা নুড়ি ও পাথরের সাহায্যে গুহার গায়ে আঁক কেটে গণনা করত। ধীরে ধীরে মানুষ গণনার বিভিন্ন পদ্ধতি আবিষ্কার করে সভ্যতার উন্নতির সঙ্গে সঙ্গে। সংখ্যা পদ্ধতির আবিষ্কারের ফলে তথ্যের উপস্থাপনা আরো সহজ হয়ে যায়। সংখ্যাবদ্ধ থেকে প্রধানত দুটি ভাগে ভাগ করা যায় –
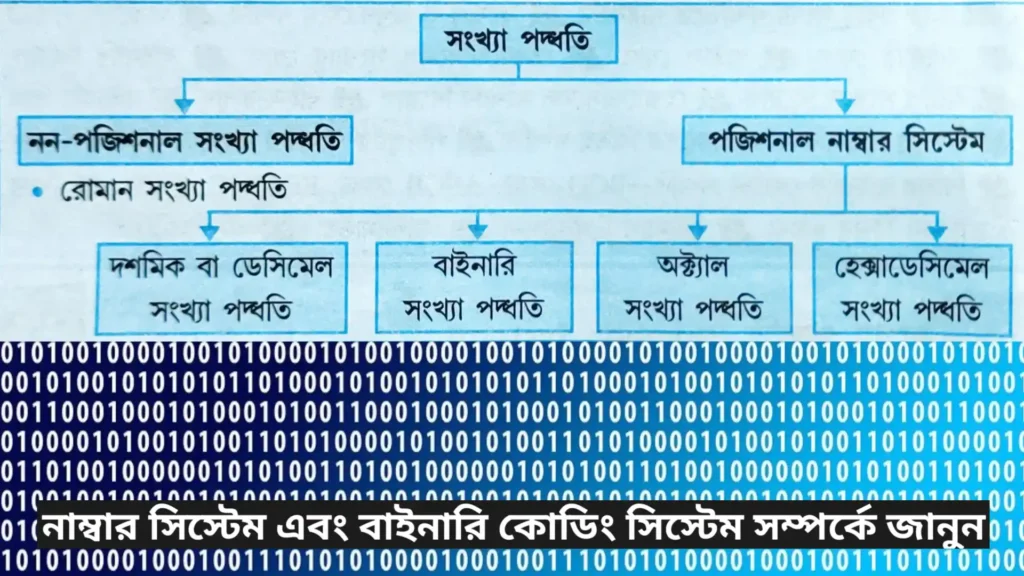
1) নন-পজিশনাল সংখ্যা পদ্ধতি (non-positional number system)
এটি একটি প্রাচীন সংখ্যা পদ্ধতি। প্রাচীনকালে মানুষ আঙুলের সাহায্যে বা নুড়ি-পাথরের সাহায্যে গণনা করতো। পরবর্তীকালে গণনার সুবিধার জন্য বিভিন্ন ধরনের চিহ্ন বা সংখ্যাসংকেত ব্যবহার করা হত। এই ধরনের চিহ্ন বা সংকেতগুলির কোন নির্দিষ্ট অবস্থান বা পজিশন ছিল না বলে একে নন-পজিশনাল সংখ্যা পদ্ধতি বলা হয়। যেমন রোমান সংখ্যা পদ্ধতি।
| ১ এর জন্য | ২ এর জন্য | ৩ এর জন্য | ৪ এর জন্য | ৫ এর জন্য | ৬ এর জন্য | |
|---|---|---|---|---|---|---|
| প্রাচীন পদ্ধতি | | | || | ||| | |||| | ||||| | ||||||||| |
| রোমান পদ্ধতি | I | II | III | IV | V | IX |
2) পজিশনাল নাম্বার সিস্টেম (positional number system)
এই পদ্ধতিতে অংকের অবস্থান পরিবর্তন করলেই সংখ্যাটির মানের পরিবর্তন হয়। কতকগুলি সংখ্যা বা চিহ্ন ব্যবহার করে সংখ্যাগুলিকে প্রকাশ করা হয়। এবং প্রত্যেকটি সংখ্যার একটি নির্দিষ্ট ব্যাস ভ্যালু বা রেডিক্স থাকে। এই পদ্ধতিতে সংখ্যাগুলির মান তাদের অবস্থানের উপর নির্ভর করে। যেমন- 578 সংখ্যাটি তিনটি অংকের (5, 7 ও 8)সমন্বয়ে গঠিত। এই সংখ্যার 5, 7 ও 8 অংক গুলি যদি স্থান পরিবর্তন করে তাহলে সংখ্যাটির মানের পরিবর্তন হয়। যেমন 578 থেকে 785 বা 875 ।
বর্তমানে সমস্ত গণনার কাজ পজিশনাল নাম্বার সিস্টেম ব্যবহার করে করা হয়। পজিশনাল নাম্বার সিস্টেম আবার চার প্রকারের হয়ে থাকে। যেমন – দশমিক (decimal), বাইনারি (binary), অক্টাল (octal), এবং হেক্সাডেসিমেল (hexadecimal)। বর্তমানে এই চার ধরনের নাম্বার সিস্টেম কম্পিউটারে সংখ্যা প্রকাশ করার জন্য ব্যবহার করা হয়।
i) দশমিক বা ডেসিমেল সংখ্যা পদ্ধতি (decimal number system)
এ পদ্ধতি পৃথিবীর সবচেয়ে প্রাচীনতম এবং বহুল প্রচলিত সংখ্যা পদ্ধতি। ডেসিমেল সংখ্যা পদ্ধতিতে দশটি মূল সংখ্যা রয়েছে, এগুলি হলো যথাক্রমে – 0,1,2,3,4,5,6,7,8,9 । ডেসিমেল সংখ্যা পদ্ধতির বেস বা রেডিক্স হল 10 (দশ)। ডেসিমেল সংখ্যা গুলিকে দুটি ভাগে ভাগ করা যায়, যথা- পূর্ণ সংখ্যা এবং ভগ্নাংশ । এই সংখ্যা পদ্ধতিতে সংখ্যার প্রতিটি অংক ও তাদের অবস্থানগত মান বা 10 এর ঘাতক যুক্ত ভারের গুণফলগুলির যোগের সমান।
পূর্ণ সংখ্যা – এইসব সংখ্যাগুলিতে কোন দশমিক থাকে না। এগুলি এক একটি স্বাভাবিক সংখ্যা। শূন্য এবং দশমিক বিহীন সমস্ত সংখ্যায় পূর্ণ সংখ্যা। যেমন- 0,1,2..99..999 ইত্যাদি। আবার এগুলি ধনাত্মক হতে পারে, আবার ঋণাত্মকও হতে পারে।
ভগ্নাংশ সংখ্যা – স্বাভাবিক সংখ্যা ছাড়া বাকি অন্যান্য সংখ্যা গুলো বিশেষ করে যে সমস্ত সংখ্যাগুলিতে দশমিক থাকে সেগুলিকে সংখ্যা বলে। যেমন- 0.234, 4.564 ইত্যাদি।
ii) বাইনারি সংখ্যা পদ্ধতি (binary number system)
এই পদ্ধতিতে দুটি অংক বা ডিজিট ‘0’ এবং ‘1’ ব্যবহার করা হয়। যেকোনো সংখ্যা এই পদ্ধতিতে ‘0’ এবং ‘1’ এর সাহায্যে প্রকাশ করা হয়। ‘0’ এবং ‘1’ এই সংখ্যা দুটিকে বিট (Bit) বলা হয়। যেকোনো বাইনারি সংখ্যার ডানদিকে বিট-টির নাম LSB (Least Significant Bit) এবং বাম দিকের বিট-টির নাম MSB (Most Significant Bit)। চারটি বিট-কে একসঙ্গে নিবল (Nibble) এবং আটটি বিট-কে একত্রে বাইট (Byte) বলে।

কম্পিউটারে গণনার এবং তথ্য সংরক্ষণে কেবলমাত্র দুটি দিশা পাওয়া যায়। এই ক্ষেত্রে তথ্যের আউটপুট হবে উচ্চ এবং নিম্ন। উচ্চ দশার ক্ষেত্রে ‘1’ এবং নিম্ন দশার ক্ষেত্রে ‘0’ ব্যবহার করা হয়। ডিজিটাল কম্পিউটার শুধুমাত্র বাইনারি সংখ্যা (0, 1) বুঝতে পারে, কারণ কম্পিউটার 0 এবং 1 এর সমন্বয়ে যাবতীয় সংকেত গ্রহণ, আত্তীকরণ, বিশ্লেষণ, সংরক্ষণ ইত্যাদি করে। তাই কম্পিউটারে বাইনারি সংখ্যা পদ্ধতি প্রয়োজন হয়ে থাকে।
| ডেসিমেল সংখ্যা পদ্ধতি | বাইনারি সংখ্যা পদ্ধতি |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
iii) অক্টাল সংখ্যা পদ্ধতি (octal number system)
এই পদ্ধতিতে 0,1,2,3,4,5,6,7, এই 8 টি ডিজিটাল এর সাহায্যে যেকোনো সংখ্যাকে প্রকাশ করা হয়। অক্টাল সংখ্যা পদ্ধতির বেস হল = 8টি।
নিচে টেবিল 2 এ ডেসিমেল, বাইনারি ও অক্টাল সম্ভব পদ্ধতির পারস্পরিক সম্পর্ক উল্লেখ করা হল-
| ডেসিমেল সংখ্যা | অক্টাল সংখ্যা | বাইনারি সংখ্যা |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | 11 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
| 8 | 10 | 1000 |
| 9 | 11 | 1001 |
| 10 | 12 | 1010 |
| 11 | 13 | 1011 |
| 12 | 14 | 1100 |
| 13 | 15 | 1101 |
অর্থাৎ ডেসিমেল সংখ্যা যেখানে 8 সেখানে অক্টাল সংখ্যা 10 এবং বাইনারি সংখ্যা 1000 হয়। কারন অক্টাল সংখ্যাতে সংখ্যা থেকে 0 থেকে 7 পর্যন্ত টোটাল 8 টি। তাই 8টি সংখ্যার পর 10 দিয়ে পুনরায় শুরু হয়।
iv ) হেক্সাডেসিমেল সংখ্যা পদ্ধতি (hexadecimal number system)
হেক্সআর্টেসিমেল সংখ্যা পদ্ধতির বেস হল 16টি। এই পদ্ধতিতে 16 টি অঙ্ক বা ডিজিট ব্যবহার করা হয়। সেগুলি হল 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
এখানে A=10, B=11, C=12, D=13, E=14, F=15 ধরা হয়।
| ডেসিমেল সংখ্যা | বাইনারি সংখ্যা | হেক্সাডেসিমেল সংখ্যা |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
B) বিভিন্ন বাইনারি কোডিং পদ্ধতি (binary coding)
i) আলফানিউমেরিক কোড
কম্পিউটারে দশটি নিউমেরিক সংখ্যা (0-9), বর্ণমালা (A-Z), 7টি যতিচিহ্ন, এবং 20 থেকে 40 টি অন্যান্য ক্যারেক্টার যেমন- #, @, &, /, – , +, % ইত্যাদি ব্যবহার করে তথ্য আদান প্রদান করা হয়। এগুলি আলফানিউমেরিক ক্যারেক্টার সেট বা আলফানিউমেরিক কোড বলা হয়।
ii) BCD কোড
BCD কোডের সম্পূর্ণরূপ হল বাইনারি কোডেড ডেসিমেল (binary coded decimal)। এই কোডিং পদ্ধতি অতীতের কিছু কম্পিউটারে ব্যবহার হতো। BCD কোডের সাহায্যে প্রতিটি ডেসিমেল ডিজিটকে চারটি গ্রুপের সাহায্যে প্রকাশ করা যায়। যেমন ডেসিমেল সংখ্যা 2 এর BCD রূপ হল 0010, আবার 9 সংখ্যাটির BCD রূপ হল 1001 ।
সাধারণত কম্পিউটারে BCD কোর্টের প্রচলন খুবই কম। বর্তমানে পকেট ক্যালকুলেটর, ভোল্টামিটার, অ্যামমিটার ইত্যাদিতে ডেসিমেল রাশিগুলিকে বোঝানোর জন্য BCD কোড ব্যবহার করা হয়।
iii) ASCII কোড
ASCII কোডের সম্পূর্ণ নাম হলো ”আমেরিকান স্ট্যান্ডার্ড কোড ফর ইনফরমেশন এন্টারচেঞ্জ”। ASCII একটি সাতটি বিটের বাইনারি কোড। এই কোডের যেকোনো সংখ্যাকে 7 বিট বাইনারি সংখ্যা দ্বারা প্রকাশ করা যায়। এই কোডের সাহায্যে সর্বাধিক 27 =128 টি ক্যারেক্টারকে প্রকাশ করা যায়। ASCII কোডের মোট ক্যারেক্টার এর সংখ্যা হল 94টি।
এগুলির মধ্যে সংখ্যা (0-9) হল 10টি , বড় হাতের ইংরেজি বর্ণমালা (A-Z) হল 26টি, ছোট হাতের ইংরেজি বর্ণমালা (A-Z) হল 26টি, এবং বিশেষ ও অন্যান্য ক্যারেক্টারের (@, #, ₹, *, /, +) সংখ্যা হল 32টি। বর্তমানে ASCII কোড সাধারণত মিনি কম্পিউটার, মাইক্রোকম্পিউটার, কিছু মেনফ্রেম কম্পিউটারে ব্যবহার হয়ে থাকে।
iv) EBCDIC কোড
EBCDIC সম্পূর্ণ নাম “এক্সটেনডেড বাইনারি কোডেড ডেসিমেল ইন্টারচেঞ্জ কোড”। এই কোডে ক্যারেক্টারগুলি প্রকাশ করা হয় 8টি বিট দিয়ে। 8 টি ডেট দিয়ে সর্বাধিক 2⁸ =256 টি ক্যারেক্টারকে প্রকাশ করা যায়। এই কোডটি সাধারণত IBM (ইন্টারন্যাশনাল বিজনেস মেশিন) মেন ফ্রেম কম্পিউটারে বেশি ব্যবহার করত।
v) ISCII কোড
ISCII কোডের সম্পূর্ণ নাম হল “ইন্ডিয়ান স্ট্যান্ডার্ড কোড ফর ইনফরমেশন এন্টারচেঞ্জ”। ভারতীয় বিভিন্ন ভাষাকে (বাংলা, তেলেগু, মালায়ালাম, হিন্দি, দেবনাগরী ইত্যাদি) কম্পিউটারাইজ করার জন্য ISCII কোড তৈরি করা হয়েছে। এটি একটি 8 টি বিযুক্ত কোড। এই কোডের সাহায্যে সর্বাধিক 2⁸ =256 টি ক্যারেক্টার প্রকাশ করা যায়। এরমধ্যে 128 টি হল মূল ISCII কোড, বাকি 128 এর মধ্যে 96 টি ভারতীয় ভাষার বর্ণমালা, এবং বাকি 32 টি অন্যান্য চিহ্ন। নির্বাচন কমিশন, আধার, ভূমি সংক্রান্ত ইত্যাদি কাজের ডেটা সংরক্ষণে ISCII কোডের ব্যবহার করা হয়।
computer number system কী?
যে সমস্ত নাম্বারের মাধ্যমে কম্পিউটারের গাণিতিক সহ বিভিন্ন সমস্যার সমাধান করা হয়, তাকে কম্পিউটার নাম্বার সিস্টেম বলে।
computer number system কত ধরনের রয়েছে?
প্রধানত দুই ধরনের। যথা নন-পজিশনাল সংখ্যা পদ্ধতি এবং পজিশনাল সংখ্যা পদ্ধতি। পজিশনাল সংখ্যা পদ্ধতিকে চার ভাগে ভাগ করা হয়। সেগুলি হল ডেসিমেল, বাইনারি, অক্টাল, হেক্সাডেসিমেল সংখ্যা পদ্ধতি।