ডিজিটাল কম্পিউটারের সমস্ত কাজ লজিক্যাল অপারেশনের দ্বারা করা হয়। এর জন্য একগুচ্ছ সিগন্যাল পাশ করানো হয় স্ট্যান্ডার্ড ব্লক যুক্ত বিল্ট-ইন সার্কিটের মধ্যে দিয়ে যা লজিক গেট নামে পরিচিত। এই লজিক গেট দ্বারা কম্পিউটারের ইলেকট্রনিক সার্কিটগুলি গঠিত হয়। লজিক গেট একটি ইলেকট্রনিক সার্কিট যা এক বা একাধিক ইনপুট সিগন্যালের থেকে স্ট্যান্ডার্ড আউটপুট সিগন্যাল তৈরি করে। বর্তমানে একাধিক বিভিন্ন ধরনের লজিক গেট ব্যবহার করে কম্পিউটারের ইলেকট্রনিক সার্কিটগুলি প্রস্তুত করা হয়।
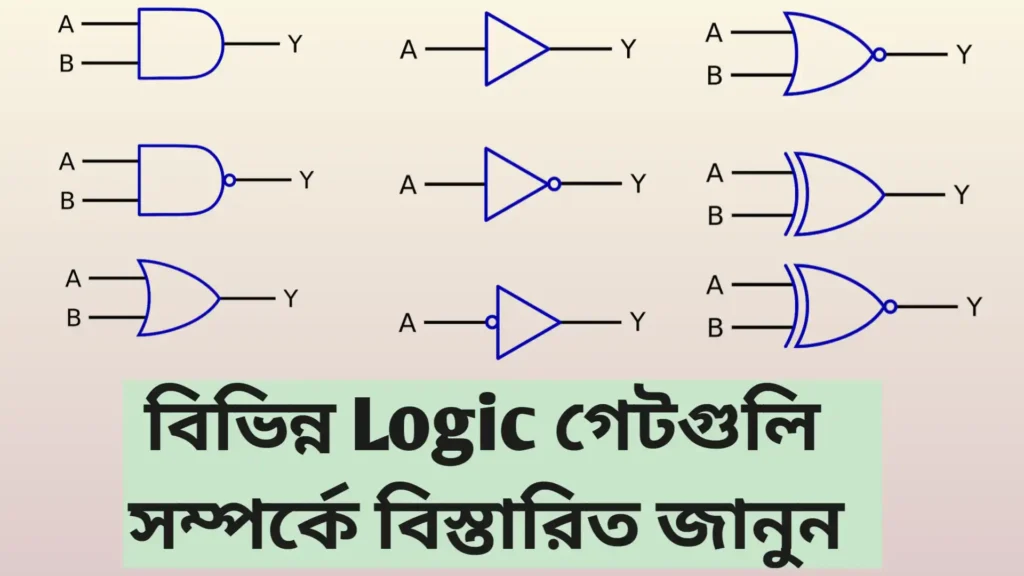
1] মৌলিক গেটসমূহ (Fundamental Gates )
তিনটি মূল গেট ব্যবহার করে যেকোনো ধরনের লজিক সার্কিটস তৈরি করা যায়। এই তিনটি গেট হল AND গেট, OR গেট এবং NOT গেট।
1.1] AND গেট (AND Gate)
যে ইলেকট্রনিক সার্কিটে দুটি বা তার অধিক সুইচ শ্রেণি সমবায়ে (Series Combination) যুক্ত থাকে এন্ড গেট (AND Gate) বলে।
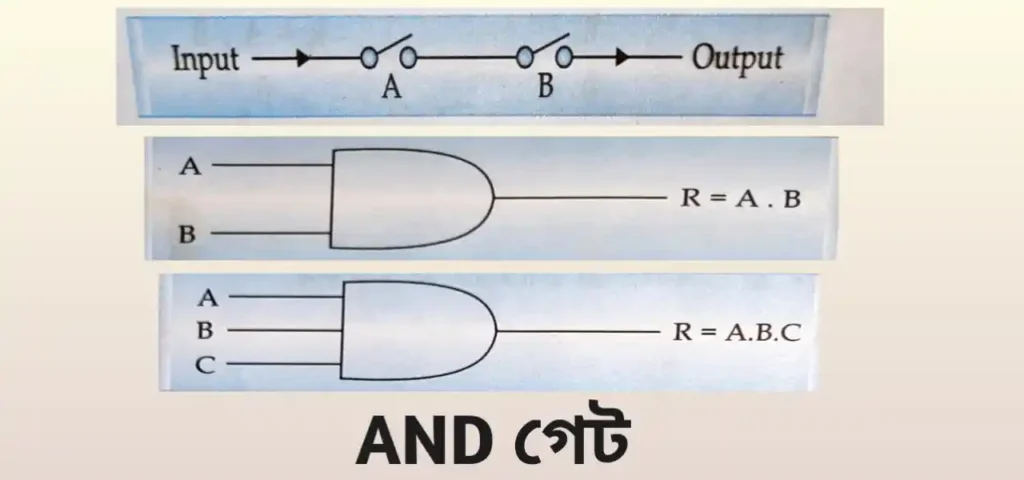
AND গেট প্রকৃতপক্ষে লজিক্যাল গুণ (.) অপারেশন। তাই AND গেটে সবকটি ইনপুট যদি 1 হয় তবে আউটপুট 1 হবে। বাকি সব ক্ষেত্রে আউটপুট 0 হবে। এক্ষেত্রে ইনপুট সংকেত দুই বা ততোধিক কিন্তু আউটপুট সংকেত হল একমাত্র একটি।
তাই ইনপুট যদি হয় A ও B , এবং আউটপুট = A.B হবে । আবার ইনপুট যদি B, B,C হয়, তাহলে আউটপুট =A.B.C হবে। এমনকি ইনপুট যদি B,B,C….N হয় তাহলে আউটপুট = A.B.C….N হবে।
AND গেটের সত্য সারণী (and gate truth table)
দুটি ইনপুট যুক্ত AND গেটের সত্য সারণী
| Input | Input | Output |
|---|---|---|
| A | B | Result (R)=A.B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
এক্ষেত্রে A AND B = A.B
তিনটি ইনপুট যুক্ত AND গেটের সত্য সারণী
| Input | Input | Input | Output |
|---|---|---|---|
| A | B | C | Result (R)=A.B.C |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
এক্ষেত্রে A AND B AND C = A.B.C
1.2] OR গেট ( OR Gate )
যে ইলেকট্রনিক সার্কিটে দুটি বা তার অধিক সুইচ সমান্তরালভাবে যুক্ত থাকে তাকে OR গেট বলে। OR ডেট হল লজিক্যাল যোগ (+) অপারেশন, তাই OR গেটে যে কোন ইনপুট 1 হলেই আউটপুট 1 হবে। একমাত্র সবকটি ইনপুট 0 হলে আউটপুট 0 হবে।
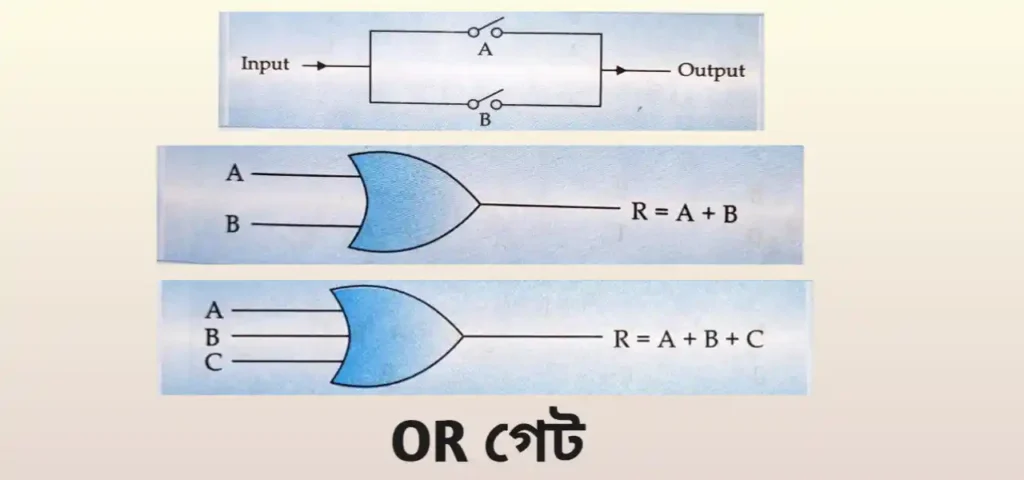
অর্থাৎ ইনপুট যদি A ও B হয়, তাহলে আউটপুট =A+B হবে। আবার ইনপুট যদি A, B, C হয় তাহলে আউটপুট = A+B+C হবে।
OR গেটের সত্য সারণী বা ট্রুথ টেবিল
দুটি ইনপুট যুক্ত OR গেটের সত্য সারণী
| Input | Input | Output |
|---|---|---|
| A | B | Result (R)=A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
তিনটি ইনপুট যুক্ত OR গেটের সত্য সারণী
| Input | Input | Input | Output |
|---|---|---|---|
| A | B | C | Result (R)=A+B+C |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
1.3] NOT গেট (NOT Gate)
NOT গেটের ক্ষেত্রে সর্বদাই একটি ইনপুট ও একটি আউটপুট থাকে। আউটপুট সর্বদা ইনপুটের ঠিক বিপরীত বা পরিপূরক হয়। NOT গেটের A ইনপুট হলে আউটপুট হবে A Complementation বা Inversion, নিচে NOT গেটের যে চিত্র দেখানো হয়েছে সেখানে A হল ইনপুট এবং R=A Complementation হল আউটপুট। NOT গেট-এর ইনপুট সর্বদাই আউটপুট-এর বিপরীত হয়। অর্থাৎ ইনপুট 1 হলে আউটপুট 0, আবার ইনপুট হলে আউটপুট 1 হবে।

NOT গেটের সত্য সারণী (not gate truth table)
একটি ইনপুট যুক্ত OR গেটের সত্য সারণী

2] ইউনিভার্সাল গেটস (universal gates)
সমস্ত প্রকার ডিজিটাল সিস্টেম AND, OR এবং NOT এই তিনটি লজিক গেটস দ্বারা তৈরি করা যায়। তাই এই তিনটি গেটকে বেসিক লজিক গেটস (Basic Logic Gates) বলা হয়। এই বেসিক গেটগুলি ব্যবহার করে আমরা যে চারটি গেট তৈরি করতে পারি, সেগুলি হল—
- (i) NAND
- (ii) NOR
- (iii) XOR এবং
- (iv) X-NOR
NAND ও NOR গেট দ্বারা AND, OR এবং NOT এই মূল গেটগুলি তৈরি করা যায়। তাই এই গেট দুটিকে ইউনিভার্সাল গেটস বলে।
2.1] NAND গেট (NAND Gate)
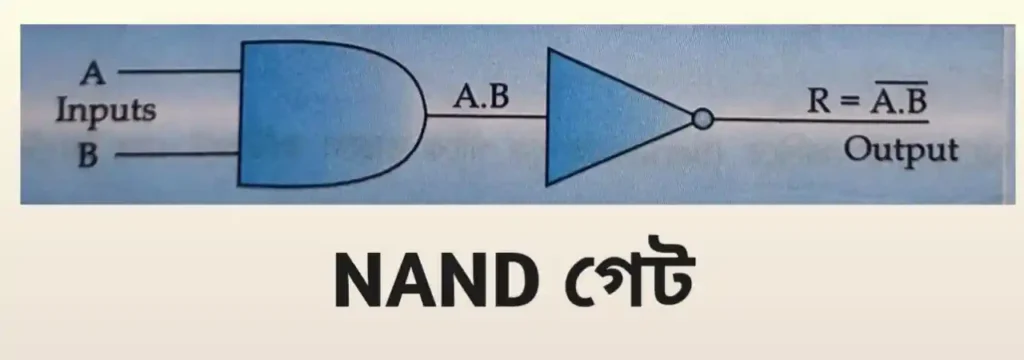
NAND গেট একটি NOT ও একটি AND গেট-এর সমন্বয়ে তৈরি হয়। অর্থাৎ NAND প্রক্রিয়া AND প্রক্রিয়ার পূরক (Complement)। AND গেটের আউটপুট লাইনে একটি ইনভার্টার অর্থাৎ NOT-গেট যুক্ত করলে NAND-গেট পাওয়া যায়।
NAND গেটের ক্ষেত্রে দুই বা ততোধিক ইনপুটের জন্য একটিমাত্র আউটপুট পাওয়া যায়। নিচের চিত্রে A ও B দুটি ইনপুট প্রথমে AND ও পরে NOT অপারেশনের পর আউটপুট R-এর মান R = A.B Complementation বা Inversion দেখানো হয়েছে।
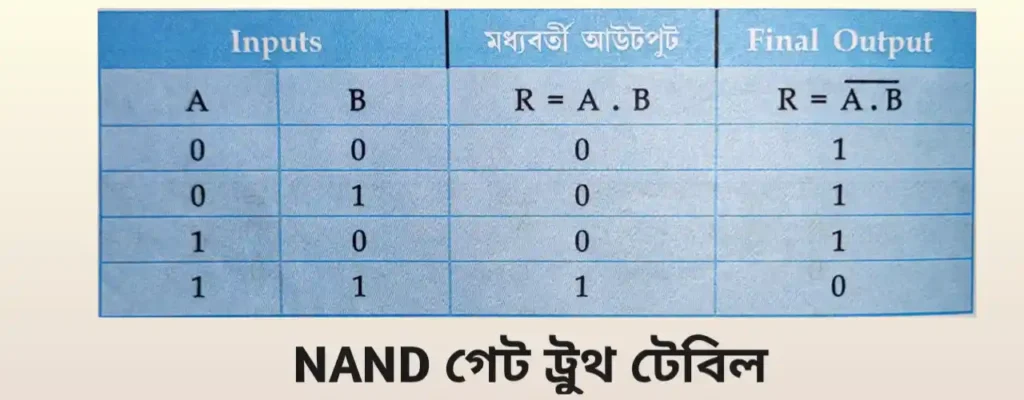
NAND গেটের সত্য সারণী
দুটি ইনপুট যুক্ত NAND গেটের সত্য সারণী
2.2] NOR গেট (NOR Gate)
একটি NOT ও একটি OR গেটের সমন্বয়ে NOR গেট তৈরি হয়। NOR গেটের ক্ষেত্রে দুই বা ততোধিক ইনপুটের জন্য একটিমাত্র আউটপুট পাওয়া যায়। অর্থাৎ NOR প্রক্রিয়া যেহেতু OR প্রক্রিয়ার পূরক, সুতরাং OR গেটের সঙ্গে একটি NOT গেট (ইনভার্টার) যুক্ত করলেই NOR গেট প্রস্তুত হয়। নিচের ছবিতে OR এবং NOR গেট ব্যবহার করে NOR গেটের নকশা এবং সেটির চিহ্ন দেখানো হল।
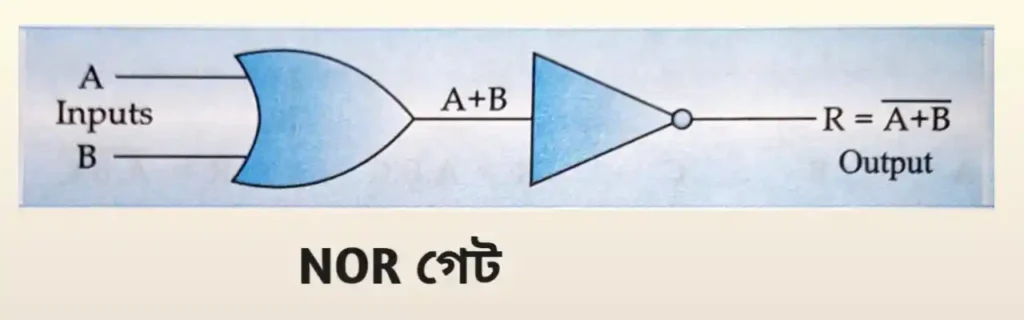
NOR গেটের ক্ষেত্রে দুই বা ততোধিক ইনপুটের জন্য একটিমাত্র আউটপুট পাওয়া যায়। উপরের চিত্রে A ও B দুটি ইনপুট প্রথমে OR ও পরে NOT অপারেশনের পর আউটপুট R-এর (Result) মান R = A+B Complementation বা Inversion দেখানো হয়েছে।
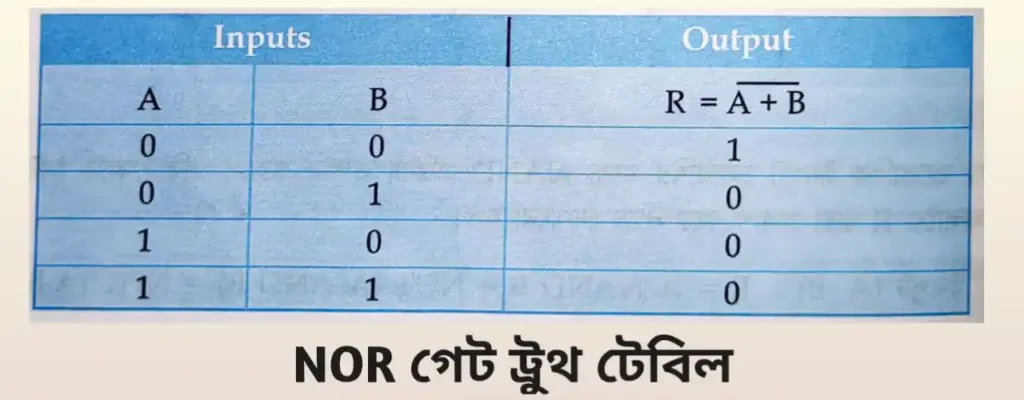
দুটি ইনপুট যুক্ত NOR গেটের সত্য সারণী নিচের টেবিলে
2.3] এক্সক্লুসিভ OR বা XOR গেট (Exclusive-OR Gate)
XOR গেটে দুটি বা তার বেশি ইনপুট থাকতে পারে কিন্তু আউটপুট সিগন্যাল একটি। বুলিয়ান বীজগণিতে ⊕ চিহ্ন দ্বারা XOR অপারেশনকে বোঝানো হয়। অতএব A XOR B-কে লেখা যায় AB। অতএব এর আউটপুট হল R (Result)= A ⊕ B = A . B Inversion + A Inversion . B
XOR প্রক্রিয়ায় ইনপুট চলরাশিগুলির মধ্যে বিজোড় সংখ্যক রাশির মান ‘1´ হলে আউটপুট হবে ‘1’ । কিন্তু জোড় সংখ্যক ইনপুট রাশির মান ‘1’ কিংবা সমস্ত ইনপুট রাশির মান ‘0 হলে আউটপুট ‘0′ হবে। A এবং B ইনপুট চলরাশি দুটি XOR প্রক্রিয়ায় যুক্ত হয়ে আউটপুট দেবে A . B Inversion + A Inversion . B যা XOR প্রতীক ‘⊕’ ব্যবহার করে A ⊕ B আকারে প্রকাশ করা যায়।
সুতরাং A এবং B-এর যেকোনো একটির (বিজোড় সংখ্যক) মান ‘1’ হলে তবেই আউটপুট ‘1’ হবে। অন্যান্য ক্ষেত্রে সর্বদাই আউটপুট ‘0’। নিচে XOR গেটের নকশা এবং সেটির প্রতীক দেখানো হল।
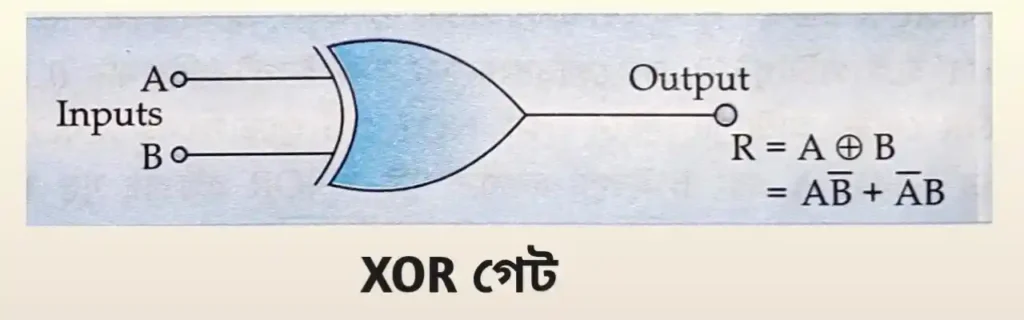
দুটি ইনপুট যুক্ত XOR গেটের সত্য সারণী নিচের টেবিলে
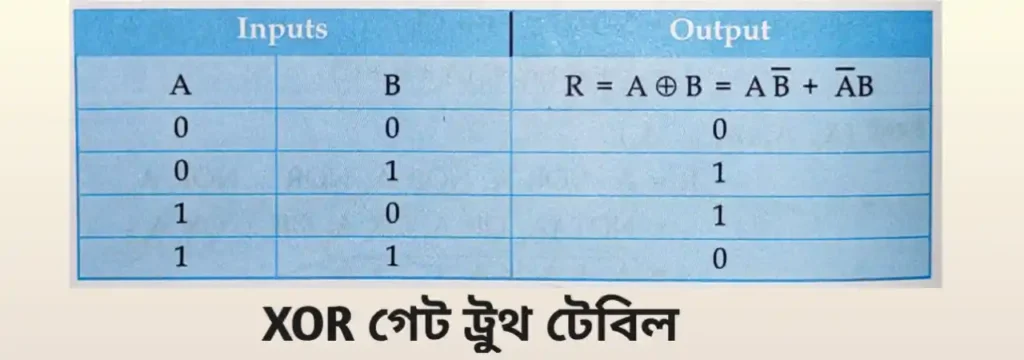
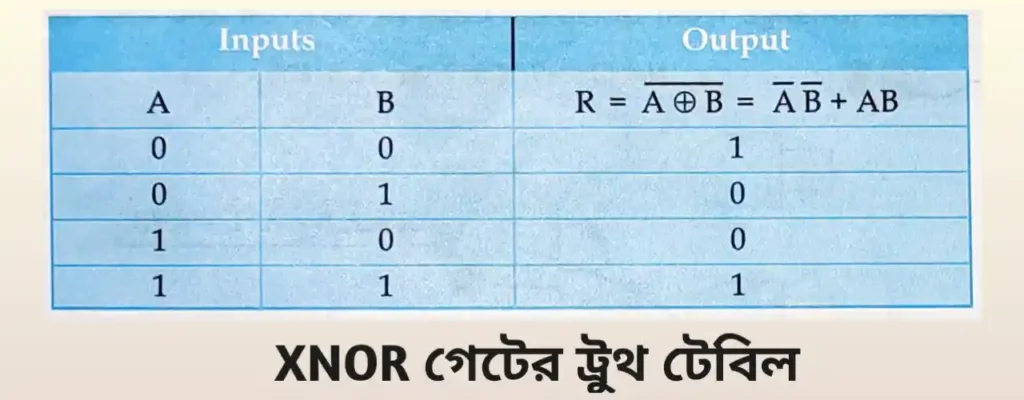
2.4] এক্সক্লুসিভ NOR বা XNOR গেট (Exclusive-NOR Gate)
XNOR প্রক্রিয়া XOR প্রক্রিয়ার পূরক এবং এটির প্রতীক ⊕ অর্থাৎ, এক্ষেত্রে বিজোড় সংখ্যক ইনপুট চলরাশির মান ‘1’ হলে আউটপুট ‘0’ এবং জোড়সংখ্যক বা সমস্ত ইনপুট রাশির মান ‘0 হলে আউটপুট ‘1’ হবে। XOR গেটের আউটপুট লাইনে একটি NOT গেট জুড়ে দিলেই XNOR গেট প্রস্তুত হয়ে যায়। A এবং B ইনপুট চলরাশি দুটি XNOR প্রক্রিয়ায় যুক্ত হয়ে আউটপুট দেয় AB + AB inversion বা A’B’ + AB যা A ⊕ B বা (A ⊕ B)´ দ্বারা প্রকাশ করা হয়।
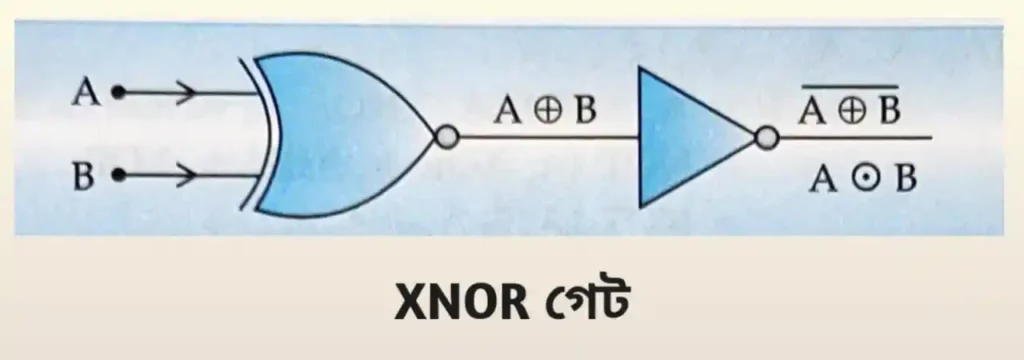
দুটি ইনপুট যুক্ত XNOR গেটের সত্য সারণী নিচের টেবিলে